Kapitel 1 Wozu brauchen wir Statistik in der Physiotherapie

Dies ist eine unvollständige und unkorrigierte Version 2022-12-24.
Dieses Kapitel soll nur ein paar wenige Anwendungsbeispiele für Statistk in der Physiotherapie aufzeigen. Sie lernen noch nichts in diesem Kapitel.
1.1 Zusammenfassen und Beschreiben
Stellen Sie sich vor, Sie möchten einen Jahresbericht für ihre Physiotherapiepraxis schreiben.
Ihr Abrechnungssystem liefert Ihnen Daten zur Anzahl gestellter Rechnungen, den gesamten in Rechnung gestellten Betrag und den durchschnittlichen Betrag pro Patient:in. Herzliche Gratulation: Das ist schon Statistik.
Sie möchten weiter wissen, wer Ihnen wie viele Patient:innen zugewiesen hat, sowie die Anzahl der Sitzungen pro Verordnung. Hier interessiert Sie neben der durchschnittlichen Anzahl auch die tiefste und die höchste Anzahl an verordneten Sitzungen pro Verordnende Person. Im Kurs werden Sie lernen, dass es einen unterschied ist, ob ich wissen möchte, das die durchschnittliche Anzahl Sitzungen sind (Mittelwert), oder was die mittlere Anzahl Sitzungen ist (Median) - d.h. die Zahl die angibt, dass 50% der Verordnungen eine geringere Anzahl Sitzungen hatten.
Aber erstellen wir doch ein paar Fake-News und simulieren ein paar Daten:
Hier laden wir die Pakete und eine Funktion, mehr Information darüber hier:.
library(tidyverse)
library(knitr)
library(kableExtra)
library(ggridges)
library(ggplot2)
library(forcats)
library(gghighlight)
length2 <- function (x, na.rm=FALSE) {
if (na.rm) sum(!is.na(x))
else length(x)
}Mit dem nächsten Befehlsabschnitt erstellen wir fünf Variablen:
- Diagnosen –> Eine Variable mit nominalen Daten
- Geschlecht –> nominale Daten, da hier nur zwei Ausprägungen erfasst werden, nennt man dies auch dichotom. Merke: heutzutage sollten wir das Geschlecht nicht mehr dichotom erfassen.
- Anzahl_Sitzungen & Anzahl Sitzungen –> Diskrete Daten, hier Anzahl-Daten (count-Daten)
- Alter –> kontinuierliche Daten, sind proportionalskaliert
- Zuweisende –> nominale Daten
Wir lernen in einem späteren Kapitel, was für unterschiedliche Daten es gibt.
Diagnosen<-rep(c("Schlaganfall", "Parkinson", "Multiple Sklerose", "Rückenschmerzen", "Nackenschmerzen", "Kreuzbandriss", "Tendinopathien", "Geriatrie", "Frakturen"), times=c(20, 5, 12, 87, 45, 7, 8, 70, 20))
Geschlecht<-sample(c("Mann", "Frau"), size=length(Diagnosen), replace=TRUE, prob=c(0.4, 0.6))
Anzahl_Sitzungen<-rpois(length(Diagnosen), lambda=1)
Anzahl_Sitzungen<-9-Anzahl_Sitzungen
Alter<-rgamma(length(Diagnosen),shape=15, scale=3)
Zuweisende<-rep(c("Dr. Strangelove", "Dr. Feelgood", "Dr. Foster", "Dr. Isles", "Dr. Zhivago", "Dr. Quinn", "Dr. Burke", "Doc Hollywood", "Dr. Adams", "Dr. Kimble", "Dr. Frankenstein", "Dr. McCoy", "Dr. Van Helsing", "Dr. Menville", "Dr. Scully", "Dr. Marvin", "Dr. Stevens", "Dr. Lecter", "Dr. Grey", "Dr. Saroyan"),
times=c(9, 2, 6, 24, 20, 4, 4, 38, 42, 11, 1, 6, 33, 26, 4, 4, 5, 8, 15,12))Die Variablen fügen wir in einen Datansatz (Data Frame) ein. Ein Data Frame ist so eine Art Excel für Statistikprogramme.
data<-data.frame(Diagnosen, Geschlecht, Anzahl_Sitzungen, Alter, Zuweisende)
DT::datatable(data, filter='top', caption='Data Frame mit den Variablen Diagnosen, Geschlecht, Anzahl_Sitzungen, Alter und Zuweisende')Welche Ärzt:innen weisen uns wie viele Patient:innen zu?
knitr::kable(summarytools::freq(data$Zuweisende,
order="freq",
round.digits = 2),
caption='Häufigkeiten der Verordnungen pro Zuweisende:n. Freq = absolute Häufigkeit, % Valid = relative Häufigkeit in Prozenten, % Valid Cum = kumulative relative Häufigkeit in Prozenten (100% = alle gültigen Werde, d.h. ohne fehlende Werte) , % Total Cum. = kumulative absolute Häufigkeit.',
digits=1)%>% kable_styling()%>%
kableExtra::scroll_box(width = "100%", height = "100%")| Freq | % Valid | % Valid Cum. | % Total | % Total Cum. | |
|---|---|---|---|---|---|
| Dr. Adams | 42 | 15.3 | 15.3 | 15.3 | 15.3 |
| Doc Hollywood | 38 | 13.9 | 29.2 | 13.9 | 29.2 |
| Dr. Van Helsing | 33 | 12.0 | 41.2 | 12.0 | 41.2 |
| Dr. Menville | 26 | 9.5 | 50.7 | 9.5 | 50.7 |
| Dr. Isles | 24 | 8.8 | 59.5 | 8.8 | 59.5 |
| Dr. Zhivago | 20 | 7.3 | 66.8 | 7.3 | 66.8 |
| Dr. Grey | 15 | 5.5 | 72.3 | 5.5 | 72.3 |
| Dr. Saroyan | 12 | 4.4 | 76.6 | 4.4 | 76.6 |
| Dr. Kimble | 11 | 4.0 | 80.7 | 4.0 | 80.7 |
| Dr. Strangelove | 9 | 3.3 | 83.9 | 3.3 | 83.9 |
| Dr. Lecter | 8 | 2.9 | 86.9 | 2.9 | 86.9 |
| Dr. Foster | 6 | 2.2 | 89.1 | 2.2 | 89.1 |
| Dr. McCoy | 6 | 2.2 | 91.2 | 2.2 | 91.2 |
| Dr. Stevens | 5 | 1.8 | 93.1 | 1.8 | 93.1 |
| Dr. Burke | 4 | 1.5 | 94.5 | 1.5 | 94.5 |
| Dr. Marvin | 4 | 1.5 | 96.0 | 1.5 | 96.0 |
| Dr. Quinn | 4 | 1.5 | 97.4 | 1.5 | 97.4 |
| Dr. Scully | 4 | 1.5 | 98.9 | 1.5 | 98.9 |
| Dr. Feelgood | 2 | 0.7 | 99.6 | 0.7 | 99.6 |
| Dr. Frankenstein | 1 | 0.4 | 100.0 | 0.4 | 100.0 |
| <NA> | 0 | NA | NA | 0.0 | 100.0 |
| Total | 274 | 100.0 | 100.0 | 100.0 | 100.0 |
1.1.1 Welche Diagnose kommt am häufigsten vor?
knitr::kable(summarytools::freq(data$Diagnosen, order="freq",
round.digits = 2),
caption='Häufigkeiten der Diagnosen', digits=1) %>%
kable_styling()%>% kableExtra::scroll_box(width = "100%", height = "100%")| Freq | % Valid | % Valid Cum. | % Total | % Total Cum. | |
|---|---|---|---|---|---|
| Rückenschmerzen | 87 | 31.8 | 31.8 | 31.8 | 31.8 |
| Geriatrie | 70 | 25.5 | 57.3 | 25.5 | 57.3 |
| Nackenschmerzen | 45 | 16.4 | 73.7 | 16.4 | 73.7 |
| Frakturen | 20 | 7.3 | 81.0 | 7.3 | 81.0 |
| Schlaganfall | 20 | 7.3 | 88.3 | 7.3 | 88.3 |
| Multiple Sklerose | 12 | 4.4 | 92.7 | 4.4 | 92.7 |
| Tendinopathien | 8 | 2.9 | 95.6 | 2.9 | 95.6 |
| Kreuzbandriss | 7 | 2.6 | 98.2 | 2.6 | 98.2 |
| Parkinson | 5 | 1.8 | 100.0 | 1.8 | 100.0 |
| <NA> | 0 | NA | NA | 0.0 | 100.0 |
| Total | 274 | 100.0 | 100.0 | 100.0 | 100.0 |
Abbildung 1.1: Quiz Häufigkeit der Diagnosen
Wir stellen die beiden Variablen Zuweisende und Diagnosen in einer Kreuztabelle dar.
summarytools::ctable(data$Zuweisende, data$Diagnosen, prop='c', style = "rmarkdown") ## ### Cross-Tabulation, Column Proportions
## #### Zuweisende * Diagnosen
## **Data Frame:** data
##
## | | | | | | | | | | | | |
## |-----------------:|----------:|------------:|------------:|--------------:|------------------:|----------------:|-----------:|----------------:|-------------:|---------------:|-------------:|
## | | Diagnosen | Frakturen | Geriatrie | Kreuzbandriss | Multiple Sklerose | Nackenschmerzen | Parkinson | Rückenschmerzen | Schlaganfall | Tendinopathien | Total |
## | Zuweisende | | | | | | | | | | | |
## | Doc Hollywood | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 38 ( 43.7%) | 0 ( 0.0%) | 0 ( 0.0%) | 38 ( 13.9%) |
## | Dr. Adams | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 25 ( 55.6%) | 0 ( 0.0%) | 17 ( 19.5%) | 0 ( 0.0%) | 0 ( 0.0%) | 42 ( 15.3%) |
## | Dr. Burke | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 4.6%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 1.5%) |
## | Dr. Feelgood | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 2 ( 10.0%) | 0 ( 0.0%) | 2 ( 0.7%) |
## | Dr. Foster | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 6 ( 30.0%) | 0 ( 0.0%) | 6 ( 2.2%) |
## | Dr. Frankenstein | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 1 ( 2.2%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 1 ( 0.4%) |
## | Dr. Grey | | 8 ( 40.0%) | 7 ( 10.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 15 ( 5.5%) |
## | Dr. Isles | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 12 (100.0%) | 0 ( 0.0%) | 5 (100.0%) | 4 ( 4.6%) | 3 ( 15.0%) | 0 ( 0.0%) | 24 ( 8.8%) |
## | Dr. Kimble | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 11 ( 24.4%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 11 ( 4.0%) |
## | Dr. Lecter | | 0 ( 0.0%) | 8 ( 11.4%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 8 ( 2.9%) |
## | Dr. Marvin | | 0 ( 0.0%) | 4 ( 5.7%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 1.5%) |
## | Dr. McCoy | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 6 ( 13.3%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 6 ( 2.2%) |
## | Dr. Menville | | 0 ( 0.0%) | 26 ( 37.1%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 26 ( 9.5%) |
## | Dr. Quinn | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 4.6%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 1.5%) |
## | Dr. Saroyan | | 12 ( 60.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 12 ( 4.4%) |
## | Dr. Scully | | 0 ( 0.0%) | 4 ( 5.7%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 4 ( 1.5%) |
## | Dr. Stevens | | 0 ( 0.0%) | 5 ( 7.1%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 5 ( 1.8%) |
## | Dr. Strangelove | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 9 ( 45.0%) | 0 ( 0.0%) | 9 ( 3.3%) |
## | Dr. Van Helsing | | 0 ( 0.0%) | 16 ( 22.9%) | 7 (100.0%) | 0 ( 0.0%) | 2 ( 4.4%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 8 (100.0%) | 33 ( 12.0%) |
## | Dr. Zhivago | | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 20 ( 23.0%) | 0 ( 0.0%) | 0 ( 0.0%) | 20 ( 7.3%) |
## | Total | | 20 (100.0%) | 70 (100.0%) | 7 (100.0%) | 12 (100.0%) | 45 (100.0%) | 5 (100.0%) | 87 (100.0%) | 20 (100.0%) | 8 (100.0%) | 274 (100.0%) |Ein Bild sagt mehr als \(10^{3}\) Worte:
ggplot(data,aes(x = fct_infreq(Zuweisende))) +
geom_bar(stat = 'count', aes(fill=fct_infreq(Diagnosen))) +
theme_classic()+
coord_flip()+
guides(fill=guide_legend(title="Diagnosen, geordnet nach Häufigkeit"))+
theme(legend.position=c(.6,.7))+ # Legend Position
labs(y="Häufigkeit", x="Zuweisende")
Abbildung 1.2: Häufigkeiten der Verordnungen, pro Zuweisende. Farblich abgegrenzt: Diagnosen.
# order data https://www.roelpeters.be/reorder-ggplot2-bar-chart-by-count/Wir können auch die Verteilung der Daten anschauen, zum Beispiel für die Variable Alter. Für eine einfache Darstellung genügt ein Befehl:
hist(Alter, col="#F54CE5", main="Histogramm des Alters")
Abbildung 1.3: Einfaches Histogramm der Variable Alter
Wir können auch komplexere Graphiken darstellen. Dazu simulieren wir wieder zusätzliche Daten.
rm(Alter)
rm(Anzahl_Sitzungen)
data<-data %>%
mutate(Alter=case_when(
Diagnosen=="Geriatrie"~rnorm(nrow(.), 75, 5),
TRUE~Alter
)) %>%
mutate(Alter=case_when(
Diagnosen=="Kreuzbandriss"&Geschlecht=="Frau"~rnorm(nrow(.), 27, 3),
TRUE~Alter)) %>%
group_by(Diagnosen) %>%
mutate(Anzahl_Sitzungen=rpois(n(), lambda=sample(size=n(),x=c(1,2, 3,5), replace=TRUE))) %>%
ungroup() %>%
mutate(Anzahl_Sitzungen=9-Anzahl_Sitzungen) %>%
mutate(Anzahl_Sitzungen=ifelse(Anzahl_Sitzungen>7, 9, Anzahl_Sitzungen),
Anzahl_Sitzungen=ifelse(Anzahl_Sitzungen<1,1, Anzahl_Sitzungen))Hier unten die graphische Darstellung dieser Daten:
data_summary <- function(x) {
mu <- median(x)
sigma1 <- quantile(x, probs=0.25)[[1]]
sigma2 <- quantile(x, probs=0.75)[[1]]
return(c(y=mu,ymin=sigma1,ymax=sigma2))
}
ggplot(data=data, aes(x=Diagnosen, y=Anzahl_Sitzungen, fill=Diagnosen)) +
geom_jitter(width = 0.2, height=0.2, aes(color=Diagnosen))+
geom_violin(draw_quantiles = TRUE, show.legend = TRUE, alpha=0.4) + stat_summary(fun.data=data_summary)+
theme_classic()+
coord_flip()+
theme(legend.position="none")+
scale_y_continuous(breaks=c(0,1,2,3,4,5,6,7,8,9))+
labs(y="Anzahl Sitzungen pro Verordnung")
Abbildung 1.4: Violinen-Plot für die Anzahl der Sitzungen pro Verordnung. Die farbigen Abschnitte gehen vom kleinsten zum grössten Wert und spiegeln die Verteilung der Häufigkeiten vor. Der schwarze Punkt entspricht dem Median und die schwarzen Striche dem Bereich von der 25. bis zur 75. Perzentile (auch 1. und 3. Quartile genannt).
Nicht immer ist eine Graphik die beste Form Daten zusammenzufassen. Wir könnten die in der Abbildung 1.1 gezeigten Daten auch in einer Tabelle zusammenfassen.
var_summary <- function(data, var) {
data %>%
summarise(N = n(),
Min = min({{ var }}),
p25=quantile({{ var }}, probs=0.25)[[1]],
Median=median({{ var}}),
p75=quantile({{ var }}, probs=0.75)[[1]],Max = max({{ var }}))
}
summary<-data %>%
group_by(Diagnosen) %>%
var_summary(Anzahl_Sitzungen)
htmlTable::htmlTable(format(data.frame(summary), digits = 2), rnames=FALSE,
caption="Tabelle 1.3: Anzahl der Verordnungen nach Diagnosen.
N = absolute Häufigkeit, Min = minimale Anzahl Verordnungen,
p25 = 25. Perzentile (1. Quartil), p75= 75. Perzentile (3.Quartil), Max= maximale Anzahl Verordnungen")| Tabelle 1.3: Anzahl der Verordnungen nach Diagnosen. N = absolute Häufigkeit, Min = minimale Anzahl Verordnungen, p25 = 25. Perzentile (1. Quartil), p75= 75. Perzentile (3.Quartil), Max= maximale Anzahl Verordnungen | ||||||
| Diagnosen | N | Min | p25 | Median | p75 | Max |
|---|---|---|---|---|---|---|
| Frakturen | 20 | 3 | 4.8 | 7.0 | 9.0 | 9 |
| Geriatrie | 70 | 1 | 5.0 | 6.0 | 9.0 | 9 |
| Kreuzbandriss | 7 | 3 | 4.5 | 5.0 | 6.0 | 7 |
| Multiple Sklerose | 12 | 1 | 4.8 | 5.5 | 9.0 | 9 |
| Nackenschmerzen | 45 | 2 | 5.0 | 7.0 | 9.0 | 9 |
| Parkinson | 5 | 7 | 7.0 | 9.0 | 9.0 | 9 |
| Rückenschmerzen | 87 | 1 | 6.0 | 7.0 | 9.0 | 9 |
| Schlaganfall | 20 | 2 | 5.8 | 7.0 | 7.5 | 9 |
| Tendinopathien | 8 | 3 | 5.5 | 7.5 | 9.0 | 9 |
Als nächstes beschreiben wir das Alter der Patient:innen nach Diagnosen. Sie werden hier die selben Daten in zwei Tabellen sehen, dies um darzustellen, dass bei der beschreibenden Statistik ein paar Entscheidungen getroffen werden müssen, z.B. welche Statistiken wir benutzen. Wir werden später lernen, wann welche Statistiken benutzt werden, um Daten zusammenzufassen.
summary_table<-data %>%
group_by(Diagnosen) %>%
dplyr::summarise(N=length(Alter),Mittelwert=mean(Alter), SD=sd(Alter), Min=min(Alter), Max=max(Alter))Oben fassen wir die Daten zusammen und stellen sie in einem Objekt, hier summary_table genannt, zur Verfügung. Dieses Objekt ist ein data frame, das wir als Tabelle ausgeben können:
htmlTable::htmlTable(format(data.frame(summary_table), digits = 2), rnames=FALSE, caption="Tabelle 1.4: Alter der Patientinnen und Patienten, nach Diagnosen")| Tabelle 1.4: Alter der Patientinnen und Patienten, nach Diagnosen | |||||
| Diagnosen | N | Mittelwert | SD | Min | Max |
|---|---|---|---|---|---|
| Frakturen | 20 | 47 | 9.5 | 33 | 63 |
| Geriatrie | 70 | 74 | 5.9 | 57 | 85 |
| Kreuzbandriss | 7 | 42 | 18.7 | 28 | 75 |
| Multiple Sklerose | 12 | 44 | 6.2 | 35 | 53 |
| Nackenschmerzen | 45 | 43 | 11.5 | 18 | 71 |
| Parkinson | 5 | 43 | 21.5 | 23 | 73 |
| Rückenschmerzen | 87 | 46 | 12.6 | 26 | 78 |
| Schlaganfall | 20 | 48 | 14.2 | 24 | 83 |
| Tendinopathien | 8 | 46 | 9.3 | 34 | 63 |
So einfach ist beschreibende Statistik. Doch wir werden lernen, dass wir nicht immer die gleichen Berechnungen durchführen können: Je nach Art und Verteilung der Daten benötigen wir andere Kennzahlen. Sie sehen in der Tabelle 1.4 Statistiken, die wir für mindestens intervallskalierte Daten benutzen, die annähernd normal verteilt sind. Die Tabelle 1.5 zeigt Statistiken, die wir für ordinale Daten (oder intervallskalierte Daten, die nicht normalverteilt sind) benutzen. Schauen Sie sich doch einmal den Median (untere Tabelle) und den Mittelwert (obere Tabelle) für die Kreuzbandrisse an. Wir sehen einen grossen Unterschied zwischen dem Median und dem Mittelwert. Wir werden lernen, solche Unterschiede zu interpretieren.
quantiles_of_interest<-c(.25, .5, .75)
summaryTable<-data %>%
group_by(Diagnosen) %>%
dplyr::summarize(across(.cols=Alter,
.fns=list(
n=length,
Min=min,
Q1=~quantile(., probs=quantiles_of_interest[1]),
Median=median,
Q3=~quantile(., probs=quantiles_of_interest[3]),
Max=max)))%>%
select(Diagnosen, Alter_n, Alter_Median, Alter_Q1, Alter_Q3, Alter_Min, Alter_Max)
names(summaryTable)<-str_remove(names(summaryTable), "Alter_")htmlTable::htmlTable(format(data.frame(summaryTable), digits = 2), rnames=FALSE, caption="Tabelle 1.5: Alter der Patientinnen und Patienten, nach Diagnosen")| Tabelle 1.5: Alter der Patientinnen und Patienten, nach Diagnosen | ||||||
| Diagnosen | n | Median | Q1 | Q3 | Min | Max |
|---|---|---|---|---|---|---|
| Frakturen | 20 | 45 | 39 | 55 | 33 | 63 |
| Geriatrie | 70 | 73 | 70 | 78 | 57 | 85 |
| Kreuzbandriss | 7 | 31 | 29 | 49 | 28 | 75 |
| Multiple Sklerose | 12 | 46 | 39 | 49 | 35 | 53 |
| Nackenschmerzen | 45 | 41 | 36 | 51 | 18 | 71 |
| Parkinson | 5 | 35 | 26 | 57 | 23 | 73 |
| Rückenschmerzen | 87 | 45 | 36 | 55 | 26 | 78 |
| Schlaganfall | 20 | 45 | 40 | 55 | 24 | 83 |
| Tendinopathien | 8 | 43 | 41 | 50 | 34 | 63 |
Nun möchten Sie im Jahresbericht etwas über die Art der Patient:innen schreiben. Die beschreibende Statistik kann Ihnen hier helfen.
(ggplot(data, aes(forcats::fct_rev(fct_infreq(Diagnosen)), fill=Diagnosen))) +
geom_bar() +
stat_count(aes(label=paste0(sprintf("%1.0f",..count..)," (", sprintf("%1.0f", ..count../sum(..count..)*100),
"%)"), y=7+..count..),
geom="text", colour="black", size=4, position=position_dodge(width=1)) +
coord_flip()+
theme_classic()+
theme(legend.position="none")+
xlab("Diagnosen")+
ylab("Anzahl")+
ylim(c(0,100))## Warning: The dot-dot notation (`..count..`) was deprecated in ggplot2 3.4.0.
## ℹ Please use `after_stat(count)` instead.
Abbildung 1.5: Absolute und relative Häufigkeit der Anzahl Patienten pro Diagnosenkategorie
1.2 Veränderungen dokumentieren
Wir wollen beobachten, wie sich unsere Patient:innen in wichtigen Problemen oder Funktionen verändern. Ohne Statistik müssten wir jede Person einzeln beschreiben, doch Sie sehen ja sicher in der Abbildung 1.5, dass man so den Überblick verliert. Da kommt uns jetzt auch die Statistik zur Hilfe: Wir können mit Statistik zusammenfassen.
data<-rio::import("pre_post_data.csv")
data<-data %>%
mutate(Abbrecher=case_when(
!is.na(Fast_Paced_Walking_Speed_mPS_t2) | !is.na(FunctionalReach_t2)~0,
TRUE~1)) %>%
mutate(Falls_per_Year=ifelse(is.na(Falls_per_Year), 0, Falls_per_Year)) %>%
select(-Total_N_Falls_t2m12)
data$Geschlecht<-plyr::revalue(data$Geschlecht, c("Homme"="Männer", "Femme"="Frauen"))
summarytools::freq(data$Geschlecht, style = "rmarkdown")## ### Frequencies
## #### data$Geschlecht
## **Type:** Character
##
## | | Freq | % Valid | % Valid Cum. | % Total | % Total Cum. |
## |-----------:|-----:|--------:|-------------:|--------:|-------------:|
## | **Frauen** | 299 | 73.83 | 73.83 | 73.83 | 73.83 |
## | **Männer** | 106 | 26.17 | 100.00 | 26.17 | 100.00 |
## | **\<NA\>** | 0 | | | 0.00 | 100.00 |
## | **Total** | 405 | 100.00 | 100.00 | 100.00 | 100.00 |names(data)## [1] "id" "Alter"
## [3] "Geschlecht" "Fast_Paced_Walking_Speed_mPS_t0"
## [5] "Fast_Paced_Walking_Speed_mPS_t1" "Fast_Paced_Walking_Speed_mPS_t2"
## [7] "FunctionalReach_t0" "FunctionalReach_t1"
## [9] "FunctionalReach_t2" "Falls_per_Year"
## [11] "Abbrecher"data_long<-data %>%
pivot_longer(cols=c(contains("Fast"), contains("Functional")),
names_to=c(".value", "timepoint"),
names_pattern="(\\D+)_(t\\d+)")
names(data_long)## [1] "id" "Alter"
## [3] "Geschlecht" "Falls_per_Year"
## [5] "Abbrecher" "timepoint"
## [7] "Fast_Paced_Walking_Speed_mPS" "FunctionalReach"ggplot(data=data_long, aes(x=timepoint, y=Fast_Paced_Walking_Speed_mPS, group=id))+
geom_line(aes(colour=factor(Abbrecher)))+
theme_classic()+
labs(colour="Therapie-Abbrecher")+
scale_color_manual(values=c("#F647F5", "#760EF5"))+
ylab("Fast Paced Walking Speed m/s")+
xlab("Zeitpunkt")+
scale_x_discrete(labels= c("Vor Therapie", "6-Monate", "12-Monate"))
Abbildung 1.6: Die Veränderung in der Fast-Paced 10 Meter Gehgeschwindigkeit ( Gehen Sie so schnell, wie es sicher möglich ist). t0 = Baseline vor dem Start der Behandlung, t1 = nach 6 Monaten Behandlung (Heimprogramm mit 6 Einzelsitzungen), t2 = 12 Monat nach Baseline, d.h. 6 Monat nach Abschluss der Behandlung.
#viridis::scale_color_viridis(discrete = TRUE, direction=1, alpha=0.9, option="viridis") # other colour options are: viridis, magma, plasma, inferno, cividis, mako, rocket, turbo, see https://cran.r-project.org/web/packages/viridis/vignettes/intro-to-viridis.htmlNun zeichnen wir die Abbildung mit den zusammenfassenden Statistiken. Die violette Linie verbindet die Mittelwerte der drei Zeitpunkte.
summary_abbrecher<-data_long %>%
group_by(timepoint, Abbrecher) %>%
summarise(Fast_Paced_Walking_Speed_mPS_mean=mean(Fast_Paced_Walking_Speed_mPS,na.rm=TRUE), Fast_Paced_Walking_Speed_mPS_sd=sd(Fast_Paced_Walking_Speed_mPS, na.rm=TRUE),
Fast_Paced_Walking_Speed_mPS_n=length2(Fast_Paced_Walking_Speed_mPS, na.rm=TRUE))data_long<-data_long %>%
mutate(Abbrecher2=Abbrecher+2)
ggplot(data=data_long, aes(x=timepoint, y=Fast_Paced_Walking_Speed_mPS))+
geom_line(aes(group=id, colour=factor(Abbrecher), alpha=0.1))+
theme_classic()+
stat_summary(fun=mean, aes(x=timepoint, y=Fast_Paced_Walking_Speed_mPS, colour=factor(Abbrecher2), group=factor(Abbrecher)), size=2,geom="line")+
scale_color_manual(values=alpha(c("#F0C1FA","#C7A6FA","#F647F5", "#760EF5"), 0.6))+
stat_summary( fun = mean,
fun.min = function(x) mean(x) - sd(x),
fun.max = function(x) mean(x) + sd(x),
aes(colour=factor(Abbrecher2)),geom="errorbar", width=0.1, position="dodge")+
theme(legend.position="none",
panel.grid.major.y = element_line(color = "grey97"))+
annotate(geom="text", x=2.515, y=1.25, label = "Nicht-Abbrecher", size = 5, colour = "#F647F5")+
annotate(geom="text", x=1.5, y=0.93, label="Therapie-Abbrecher", size=5, colour="#760EF5")+
annotate(geom="text", x=2.3, y=0.15, label="Fehlerbalken: \u00B1 Standardabweichung", colour="#574C4B")+
ylab("Fast Paced Walking Speed m/s")+
xlab("Zeitpunkt")+
scale_x_discrete(labels= c("Vor Therapie", "6-Monate", "12-Monate"))+
scale_y_continuous(limits=c(0,3), breaks=seq(0,3,0.5))+
annotate(geom="text", label=(paste0("n = ", summary_abbrecher$Fast_Paced_Walking_Speed_mPS_n[[1]])), x=0.85, y=1.1, color="#F647F5")+
annotate(geom="text", label=(paste0("n = ", summary_abbrecher$Fast_Paced_Walking_Speed_mPS_n[[2]])), x=0.85, y=1.0, color="#760EF5")+
theme(axis.title=element_text(colour="#574C4B")) schönere Farben auswählen. Aber beachten Sie, dass über 8% der Männer und etwa 0.5% Frauen eine Farbenblindheit haben. Befolgen Sie einfach diese [Ratschläge: http://bconnelly.net/posts/creating_colorblind-friendly_figures/](http://bconnelly.net/posts/creating_colorblind-friendly_figures/). Ihr könnt eure Graphik auch testen, ob sie für Farbenblinde geeignet ist [https://www.color-blindness.com/coblis-color-blindness-simulator/](https://www.color-blindness.com/coblis-color-blindness-simulator/)](01-intro_files/figure-html/Spagetthiplot2-1.png)
Abbildung 1.7: Werte der Gehgeschwindgkeit vor und nach der Therapie sowie nach 12 Monaten. Natürlich sollten Sie mit https://color.adobe.com/create/color-wheel schönere Farben auswählen. Aber beachten Sie, dass über 8% der Männer und etwa 0.5% Frauen eine Farbenblindheit haben. Befolgen Sie einfach diese Ratschläge: http://bconnelly.net/posts/creating_colorblind-friendly_figures/. Ihr könnt eure Graphik auch testen, ob sie für Farbenblinde geeignet ist https://www.color-blindness.com/coblis-color-blindness-simulator/
Zusätzlich zu der visuellen Darstellung möchten wir die beschreibende Statistik noch in Zahlen sehen.
library(gtsummary)
data_for_table<-data_long %>%
select(Alter, Geschlecht, Abbrecher, timepoint, Fast_Paced_Walking_Speed_mPS) %>%
mutate(Abbrecher=factor(Abbrecher, levels=c(0,1), labels=c("Nicht-Abbrecher", "Abbrecher"))) %>%
mutate(Gruppen=paste(timepoint, Abbrecher, sep="-")) %>%
select(-timepoint, -Abbrecher)data_for_table %>% tbl_summary(by=Gruppen,
missing_text = "Fehlende, N:",
label=Fast_Paced_Walking_Speed_mPS~"Fast Paced Walking Speed, m/s",
statistic = list(all_continuous() ~ "{mean} ({sd})"))| Characteristic | t0-Abbrecher, N = 2301 | t0-Nicht-Abbrecher, N = 1751 | t1-Abbrecher, N = 2301 | t1-Nicht-Abbrecher, N = 1751 | t2-Abbrecher, N = 2301 | t2-Nicht-Abbrecher, N = 1751 |
|---|---|---|---|---|---|---|
| Alter | 80 (7) | 78 (6) | 80 (7) | 78 (6) | 80 (7) | 78 (6) |
| Geschlecht | ||||||
| Frauen | 168 (73%) | 131 (75%) | 168 (73%) | 131 (75%) | 168 (73%) | 131 (75%) |
| Männer | 62 (27%) | 44 (25%) | 62 (27%) | 44 (25%) | 62 (27%) | 44 (25%) |
| Fast Paced Walking Speed, m/s | 1.02 (0.36) | 1.09 (0.32) | 1.01 (0.37) | 1.16 (0.36) | NA (NA) | 1.15 (0.39) |
| Fehlende, N: | 0 | 0 | 135 | 3 | 230 | 3 |
| 1 Mean (SD); n (%) | ||||||
1.3 Zusammenhänge darstellen
Oft wollen wir verstehen, wie Dinge zusammenhängen. Es könnte uns zum Beispiel interessieren, ob es einen Zusammenhang zwischen dem 10-Meter Fast-Paced Gehtest und dem Functional Reach Test gibt. Visuell können wir das mit einem Streudiagramm (Scatterplot) darstellen. Eine Regressionslinie hilft uns, den Zusammenhang noch besser zu sehen. Die Regressionslinie steigt, es besteht also eine positive Korrelation. Positiv bedeutet hier, dass schnellere Personen auch einen besseren Functional Reach Test haben. Die Korrelation können wir auch mit einer Zahl ausdrücken, hier als Pearson’s r. Wer mehr zu Korrelationen wissen möchte, findet hier ein Video
Wichtig ist: Findet man eine Korrelation, bedeutet dies noch nicht, dass ein kausaler Zusammenhang besteht.
.
ggplot(data=data, aes(x=Fast_Paced_Walking_Speed_mPS_t0,FunctionalReach_t0))+
geom_point(aes(color=Alter))+
geom_smooth(method="lm")+
theme_classic()+
scale_color_continuous(trans = 'reverse')+
ggpubr::stat_cor(method = "pearson", label.x = 1.5, label.y = 70, p.accuracy = 0.001)
Abbildung 1.8: Streudiagramm Functional Reach Test versus Fast-Paced Gehgeschwindigkeit. Regressionslinie mit 95% Konfidenzintervall-Band. R=Pearson’s Korrelationskoeffizient.
Oder wir möchten wissen, ob ältere Personen langsamer gehen. Jetzt sinkt die Regressionslinie, wir haben also eine negative Korrelation. Je älter die Personen, desto langsamer gehen sie.
Wir sehen in der nächsten Graphik auch die Formel zu der Regressionslinie. Am Ende des Statistikkurses sollten wir diese Formel alle interpretieren können. Hier nur kurz: Eine Person mit 0 Jahren würde mit 2.5 m/s starten und dann pro Jahr 0.019 m/s langsamer werden. Natürlich dürfen wir bei solchen Regressionslinien nie über die Daten hinaus extrapolieren, d.h. wir dürfen hier keine Aussage über Personen jünger als etwa 65 Jahre machen. Die Aussage zu den Personen mit 0 Jahren ist also nur eine theoretische Aussage, die keine praktische Relevanz hat. Wenn wir Daten von jüngeren Personen anschauen würden, sähen wir, dass dort die Gehgeschwindigkeit kaum sinkt.
ggplot(data=data, aes(x=Alter,y=Fast_Paced_Walking_Speed_mPS_t0))+
geom_point(aes(color=Alter))+
geom_smooth(method="lm")+
theme_classic()+
scale_color_continuous(trans = 'reverse')+
ggpubr::stat_cor(method = "pearson", label.x = 90, label.y = 1.6, p.accuracy = 0.001)+
ggpubr::stat_regline_equation(label.y = 1.75, aes(label = ..eq.label..))
Abbildung 1.9: Streudiagramm Fast-Paced Gehgeschwindigkeit über das Alter. Mit Regressionslinie und 95% Konfidenzintervallband. R=Pearson’s Korrelationskoeffizient. Y = Regressionsformel. Daten aus einer Studie von Gaby Mittaz-Hager, Nicolas Mathieu und Roger Hilfiker.
data<-data %>%
mutate(Stürzer=ifelse(Falls_per_Year>0, 1, 0))
set.seed(123345)
sample<-data[sample(nrow(data), 200), ]Wir könnten auch untersuchen, ob Frauen häufiger Stürzen als Männer. In der folgenden Tabelle sehen wir, dass 35.3% der Frauen stürzen und 28.0% der Männer.
# summarytools::ctable(sample$Geschlecht, sample$Stürzer, style='rmarkdown')1.4 Interpretieren von wissenschaftlichen Studien
Physiotherapeutinnen und Physiotherapeuten lesen regelmässig wissenschaftliche Studien. Hierzu ist ein nötig, die wichtigsten Analysen interpretieren zu können. Zum Beispiel in Abbildung 1.9 die Forest Plots aus einem veröffentlichten Artikel Vialleron T, Delafontaine A, Ditcharles S et al. Effects of stretching exercises on human gait: a systematic review and meta-analysis [version 2; peer review: 2 approved, 1 approved with reservations]. F1000Research 2020, 9:984 (https://doi.org/10.12688/f1000research.25570.2).
knitr::include_graphics("https://f1000researchdata.s3.amazonaws.com/manuscripts/30366/482d7fe1-0218-4599-9747-4f1a5a59b00e_figure2.gif ")) über Stretching und dessen Wirkung auf Gangparameter](https://f1000researchdata.s3.amazonaws.com/manuscripts/30366/482d7fe1-0218-4599-9747-4f1a5a59b00e_figure2.gif )
Abbildung 1.10: Forest Plot aus einer systematischen Review und Meta-Analyse über Stretching und dessen Wirkung auf Gangparameter
Wir werden also in diesem Kurs etwas über Meta-Analysen lernen müssen.
knitr::include_graphics("https://bjsm.bmj.com/content/bjsports/52/10/651/F4.large.jpg?width=800&height=600&carousel=1")
Abbildung 1.11: Forest Plot der Behandlungen gegen Müdigkeit bei Krebs; Vergleich aller Behandlungen gegen Usual-Care
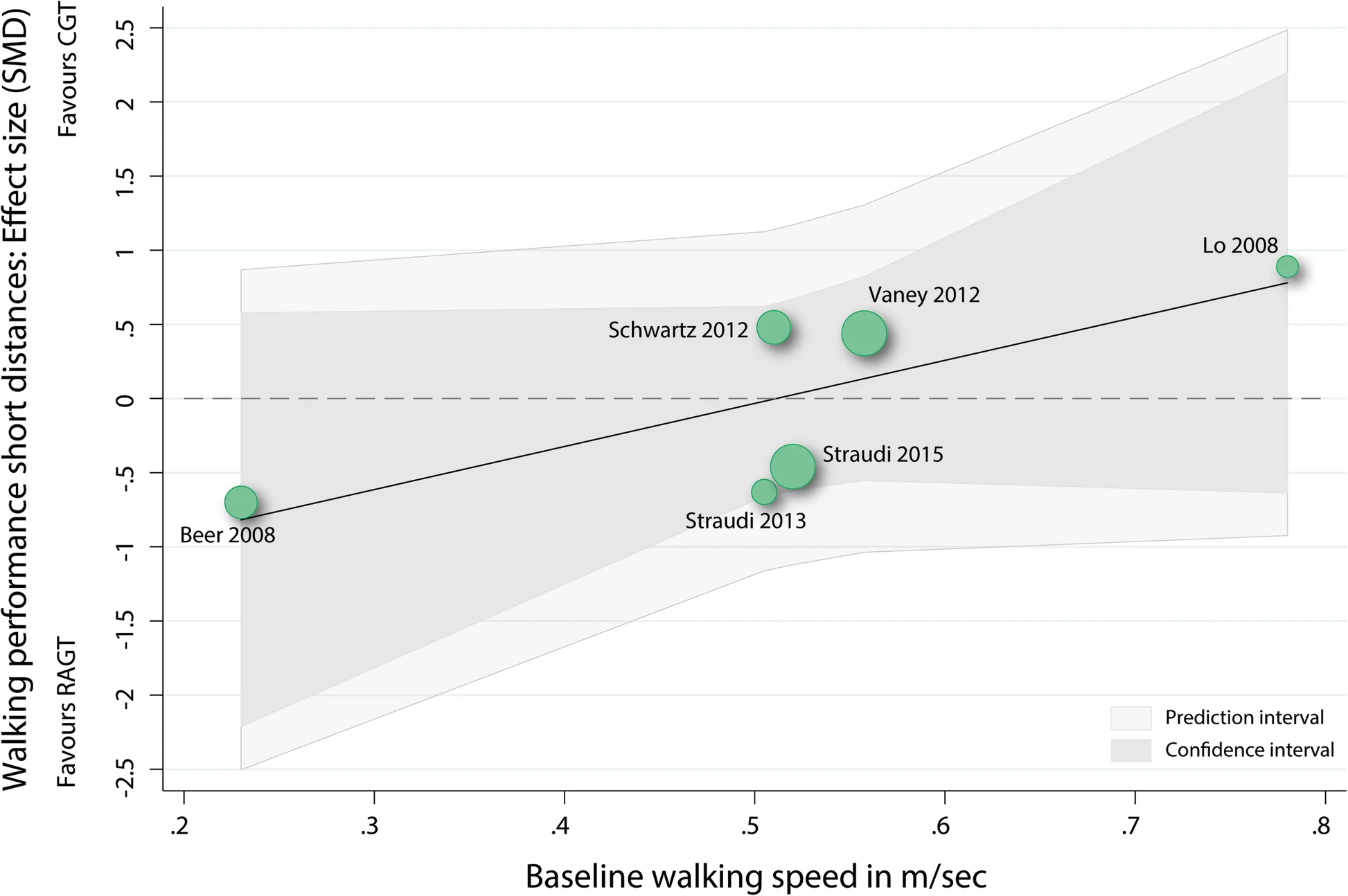
Abbildung 1.12: Meta-Regression des Effektes von Gehtraining mit Hilfsmitteln versus normales Gehtraining in Bezug zur Gehgeschwindigkeit vor der Therapie
Moderne Hilfsmittel können auch helfen, interaktive Visualisierungen und Analysen zu erstellen. In diesem Beispiel kann die Meta-Analyse des obigen Beispiels interaktiv geändert werden (Link zum Beispiel Robot-assisted gait training versus conventional overground walking for people with MS).
Abbildung 1.13: Eingebettete Webseite von Martin Sattelmayer mit Beispiel interaktiver Datenanalyse. Für eine bessere Ansicht bitte auf Link oberhalb der Graphik klicken.
Natürlich gibt es viele weitere Anwendungsgebiete für die Statistik in der Physiotherapie, doch bevor wir uns noch mehr Beispiel anschauen, müssen wir ein paar Begriffe lernen. Das tun wir in den nächsten Kapiteln.

Ende des Kapitels